This article originally appeared in Dev.Mag Issue 29, released in February 2009.

Last month we covered some of the very basic ways of testing whether object A hits object B. But, while the techniques we covered could quite likely take you very far, you’ll inevitably encounter a time when they simply aren’t enough. So this month we’ll go a little further.

Line-Line intersection test revised

Occasionally, you’ll need slightly more information from your collision tests. Many physical applications will require the precise coordinates of the intersection between lines. Thankfully, this is the easiest test to get that information.

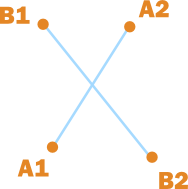
Referring back to last month, we had defined P_a and P_b as points on the respective lines that we were testing as below:

\(P_a = A_1 + u_a(A_2 – A_1)\)

and

\(P_b = B_1 + u_b(B_2 – B_1)\)

We then solved for points \(u_a\) and \(u_b\), or, rather, simply for their denominators to determine their existence. To calculate the precise point of intersection, you’d simply have to calculate and substitute one of these values into the equations for \(P_a\) or \(P_b\) (it doesn’t matter which, they’d be identical) to get your answer. Adjusting our code from last time results in the following:

LineLineCollision
Input
	LineA1	Point	First point on line A
	LineA2	Point	Second point on line A
	LineB1	Point	First point on line B
	LineB2	Point	Second point on line B
Output
	The point of the collision, or null if no collision exists.
Method
	denom = ((LineB2.Y – LineB1.Y) * (LineA2.X – LineA1.X)) –
		((LineB2.X – LineB1.X) * (LineA2.Y - LineA1.Y))
	if (denom == 0)
		return null
	else
		ua = (((LineB2.X – LineB1.X) * (LineA1.Y – LineB1.Y)) –
			((LineB2.Y – LineB1.Y) * (LineA1.X – LineB1.X))) / denom
		/* The following 3 lines are only necessary if we are checking line
			segments instead of infinite-length lines */
		ub = (((LineA2.X – LineA1.X) * (LineA1.Y – LineB1.Y)) –
			((LineA2.Y – LineA1.Y) * (LineA1.X – LineB1.X))) / denom
		if (ua < 0) || (ua > 1) || (ub < 0) || (ub > 1)
			return null

		return LineA1 + ua * (LineA2 – LineA1)

Circle-line intersection test

This is another common test that should find a use in many games. Did your ball collide with the wall of the level, or a barrier set up by the enemy? Things like that require a circular object to be tested against a line.

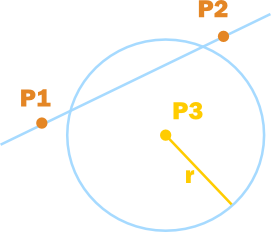
This test involves slightly longer equations than previous intersections, but is still in familiar algebraic and geometric ground. And, in fact, the expressions may be simplified greatly by the simple act of working in the circle’s local space, effectively removing all circle-centre variables from the equations by setting them all to zero. This is achieved simply by expressing the two coordinates representing the line as positions relative to the centre of the circle. Doing this makes your calculations and equations far simpler.

Using the familiar equation, we define a point P on the line as:

$$P = P_1 + u(P_2 – P_1),$$

with \(u_a\) being any real number, and \(P_1\) and \(P\) being represented in the circle’s local space.

And we define the sphere centred on the origin as:

$$x^2 + y^2 = r^2.$$

Substituting the equation of the line into the equation for the circle results in an equation in the following familiar form:

$$au^2 + bu + c = 0$$

Where \(a\), \(b\) and \(c\) are:

$$a = (x_2 – x_1)^2 + (y_2 – y_1 )^2$$

$$b = 2(x_1 (x_2 – x_1 ) + y_1 (y_2 – y_1 ))$$

$$c = x_1^2 + y_1^2 – r^2$$

Recalling some old high school algebra, the solution to such a quadratic equation is determined by the quadratic formula:

$$u = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$$

And the existence of a solution is defined by the delta, or the expression under the square root:

$$b^2 – 4ac$$

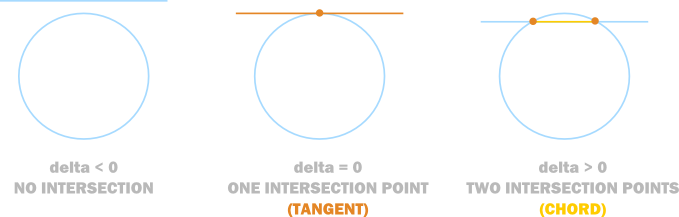
If this expression is less than 0, there is no intersection, if it exactly 0, the line is a tangent to the circle, and if it is greater than 0, the line intersects at two points.

Once this has been determined, you can substitute the value(s) for u into the equation for the line to determine the exact coordinates of the intersection. And, similar to the line – line intersection test, you can use this u value to determine whether or not the intersection occurs on the line – segment between points \(P_1\) and \(P_2\) .

In pseudocode, this technique may be implemented as follows:

CircleLineCollision
Input
	LineP1	Point	First point describing the line
	LineP2	Point	Second point describing the line
	CircleCentre	Point	The centre of the circle
	Radius	Floating-point	The circle's radius
Output
	The point(s) of the collision, or null if no collision exists.
Method
	// Transform to local coordinates
	LocalP1 = LineP1 – CircleCentre
	LocalP2 = LineP2 – CircleCentre
	// Precalculate this value. We use it often
	P2MinusP1 = LocalP2 – LocalP1 

	a = (P2MinusP1.X) * (P2MinusP1.X) + (P2MinusP1.Y) * (P2MinusP1.Y)
	b = 2 * ((P2MinusP1.X * LocalP1.X) + (P2MinusP1.Y * LocalP1.Y))
	c = (LocalP1.X * LocalP1.X) + (LocalP1.Y * LocalP1.Y) – (Radius * Radius)
	delta = b * b – (4 * a * c)
	if (delta < 0) // No intersection
		return null;
	else if (delta == 0) // One intersection
		u = -b / (2 * a)
		return LineP1 + (u * P2MinusP1)
		/* Use LineP1 instead of LocalP1 because we want our answer in global
		   space, not the circle's local space */
	else if (delta > 0) // Two intersections
		SquareRootDelta = sqrt(delta)

		u1 = (-b + SquareRootDelta) / (2 * a)
		u2 = (-b - SquareRootDelta) / (2 * a)

		return { LineP1 + (u1 * P2MinusP1) ; LineP1 + (u2 * P2MinusP1)}

That’s as far as we’ll go for this tutorial. The above techniques should be able to solve most of your problems. With clever application of the line-line segment intersection test, you could even determine the intersections between any polygons, even transformed ones. Most specific problems have more efficient solutions, but that one can solve most of them in a simple, though perhaps inefficient, way.

Good luck, and make great games without needing to compromise collision accuracy anymore. And remember, when in doubt, as long as it looks fair to the player, you can usually get away with a few tricks.