(Originally appeared in Dev.Mag Issue 20, released in February 2008.) Perlin noise is the foundation of many procedural texture and modelling algorithms. It can be used to create marble, wood, clouds, fire, and height maps for terrain. It is also very useful for tiling grids to simulate organic regions, and blending textures for interesting transitions. In this article I will explain how to implement Perlin noise, and how you can use it in your games.

Edit 19 June 2011: The examples were originally given in pseudo-code. Unfortunately, these contained some mistakes, which many commenters helped to sort out. I finally replaced the pseudo-code with real C#, copied-and-pasted from a working file (which you can download below). Hopefully it will make the algorithms easier to understand. Note that efficiency was not considered at all; the code is a fairly direct translation of the original pseudo-code.

Edit 19 May 2012: I always thought the cloudy noise described in this article is called Perlin noise. Turns out, it is not. The worst is, I cannot say with hundred percent confidence what it is called. Fractional Brownian Motion (fBm) seems to be the most likely candidate, but to be honest, I am still figuring out whether my simulation is technically equivalent to the ones described on Wikipedia (nevermind that Wikipedia may also have it wrong).

Real Classical Perlin noise, and simplex noise, can also be combined, just like the “smooth noise” is combined in this article, to give cloudy noise. This is what confused me (and others, I presume). Cloudy noise generated from Perlin noise looks much better (it is not as blocky), although for many purposes the cloudy noise described here will work fine. So if you are interested in how to make cloudy noise… read on. I will follow up at a later stage with more concrete information about real Perlin noise.

Implementation

Written in its concise mathematical form, the Perlin noise generation seems daunting, but it is actually easy to implement. There are two steps:

1. Generate a number of arrays containing “smooth” noise. Each array is called an octave, and the smoothness is different for each octave. (See the first 7 images in Figure 1).
2. Blend these together. The result is the last image in Figure 1.

That’s it! Let’s look at each of these two steps.

Wavelength: 64 Frequency: 0.015625	Wavelength: 32 Frequency: 0.03125	Wavelength: 16 Frequency: 0.0625	Wavelength: 8 Frequency: 0.125
Wavelength: 4 Frequency: 0.25	Wavelength: 2 Frequency: 0.5	Wavelength: 1 Frequency: 1	Perlin noise

Figure 1

Generating Smooth Noise

First, you need to create an array with random values between 0 and 1. This array must be the same size as the array of Perlin noise you need.

float[][] GenerateWhiteNoise(int width, int height)
{
    Random random = new Random(0); //Seed to 0 for testing
    float[][] noise = GetEmptyArray(width, height);
 
    for (int i = 0; i < width; i++)
    {
        for (int j = 0; j < height; j++)
        {
            noise[i][j] = (float)random.NextDouble() % 1;
        }
    }
 
    return noise;
}

For creating the kth octave, sample the noise array at every point (i*2^k, j*2^k) , for all i, j, and interpolate the other points linearly. The value 2^k is called the wave length of that octave, and the value 1/2^k is called the frequency.

The following pseudo C snippet shows how the kth octave is generated. Index variables are integers, and remember that integer division gives a floored integer result (for example, 5 / 3 gives 1).

float[][] GenerateSmoothNoise(float[][] baseNoise, int octave)
{
   int width = baseNoise.Length;
   int height = baseNoise[0].Length;
 
   float[][] smoothNoise = GetEmptyArray(width, height);
 
   int samplePeriod = 1 << octave; // calculates 2 ^ k
   float sampleFrequency = 1.0f / samplePeriod;
 
   for (int i = 0; i < width; i++)
   {
      //calculate the horizontal sampling indices
      int sample_i0 = (i / samplePeriod) * samplePeriod;
      int sample_i1 = (sample_i0 + samplePeriod) % width; //wrap around
      float horizontal_blend = (i - sample_i0) * sampleFrequency;
 
      for (int j = 0; j < height; j++)
      {
         //calculate the vertical sampling indices
         int sample_j0 = (j / samplePeriod) * samplePeriod;
         int sample_j1 = (sample_j0 + samplePeriod) % height; //wrap around
         float vertical_blend = (j - sample_j0) * sampleFrequency;
 
         //blend the top two corners
         float top = Interpolate(baseNoise[sample_i0][sample_j0],
            baseNoise[sample_i1][sample_j0], horizontal_blend);
 
         //blend the bottom two corners
         float bottom = Interpolate(baseNoise[sample_i0][sample_j1],
            baseNoise[sample_i1][sample_j1], horizontal_blend);
 
         //final blend
         smoothNoise[i][j] = Interpolate(top, bottom, vertical_blend);
      }
   }
 
   return smoothNoise;
}

Note that the line:

int sample_i0 = (i / samplePeriod) * samplePeriod;

is not the same as

int sample_i0 = i;

because the division automatically floors the result to give an integer, so that sample_i0 is the largest multiple of the samplePeriod dmaller than i. For example, if i is 7 and samplePeriod is 3, then sample_i0 is 6.

The following function returns a linear interpolation between two values. Essentially, the closer alpha is to 0, the closer the resulting value will be to x0; the closer alpha is to 1, the closer the resulting value will be to x1.

float Interpolate(float x0, float x1, float alpha)
{
   return x0 * (1 - alpha) + alpha * x1;
}

There are a variety of interpolation schemes; the best one to use depends on your application.

See here for some common interpolation schemes.

Blending the Arrays

To make the final array, you add weighted values of all the smooth noise arrays together. The weight used for each octave is called the amplitude.

Any values can be used for the amplitudes, with different effects. A good starting point is to use a weight of 0.5 for the first octave, 0.25 for the next octave, and so on, multiplying the amplitude with 0.5 in each step. In this scheme, the value 0.5 is called the persistence of the noise.

After you have added all the noise values, you should normalise it by dividing it by the sum of all the amplitudes, so that all noise values lie between 0 and 1.

float[][] GeneratePerlinNoise(float[][] baseNoise, int octaveCount)
{
   int width = baseNoise.Length;
   int height = baseNoise[0].Length;
 
   float[][][] smoothNoise = new float[octaveCount][][]; //an array of 2D arrays containing
 
   float persistance = 0.5f;
 
   //generate smooth noise
   for (int i = 0; i < octaveCount; i++)
   {
       smoothNoise[i] = GenerateSmoothNoise(baseNoise, i);
   }
 
    float[][] perlinNoise = GetEmptyArray(width, height);
    float amplitude = 1.0f;
    float totalAmplitude = 0.0f;
 
    //blend noise together
    for (int octave = octaveCount - 1; octave >= 0; octave--)
    {
       amplitude *= persistance;
       totalAmplitude += amplitude;
 
       for (int i = 0; i < width; i++)
       {
          for (int j = 0; j < height; j++)
          {
             perlinNoise[i][j] += smoothNoise[octave][i][j] * amplitude;
          }
       }
    }
 
   //normalisation
   for (int i = 0; i < width; i++)
   {
      for (int j = 0; j < height; j++)
      {
         perlinNoise[i][j] /= totalAmplitude;
      }
   }
 
   return perlinNoise;
}

In practice smooth noise arrays are not actually created; rather, the noise is calculated and added to the final array on the fly. How this is done is not shown here; check out the link at the end of the article for a link to example code.

Perlin noise can sometimes look diluted. For many applications this is fine; however, sometimes you might want something a bit more dramatic. This can easily be achieved in one of the following ways:

• Increase the contrast as a post-processing step using image editing software.
• Use a higher persistence (0.7 is good for 6 octaves), and skip the normalisation step. Just make sure to clamp your final values to 1.

The first method is better when you want tight visual control. The second method is more convenient as it is part of the creation process and can hence be better automated.

For more implementation tips, see Implementing and Debugging the Perlin Noise Algorithm.

Applications

Textures

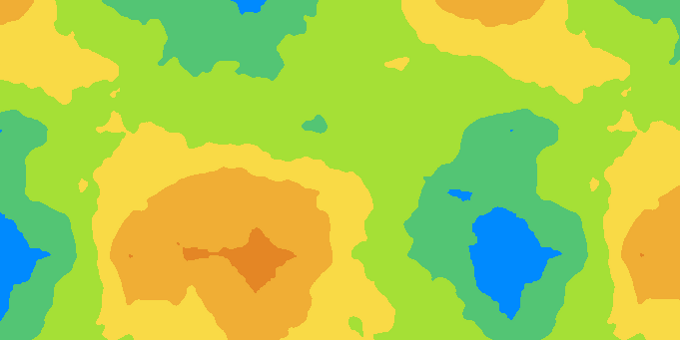
One of the simplest uses of Perlin noise is to map it with a gradient. This can be used for attractive maps or cheesy fire effects (which you can animate – explained in another section) as shown in Figure 2. You can do this with your image editor, or programmatically. For the latter approach, you need a gradient function that returns a colour given a number between 0 and 1. This function is then called for every element in you Perlin noise array to obtain a colour, which you can store in a separate array, from which an image can be created.

Grayscale gradient

Gradient with discrete colours

Fire gradient

Figure 2

Here is a code snippet showing how it works:

Color GetColor(Color gradientStart, Color gradientEnd, float t)
{
    float u = 1 - t;
 
    Color color = Color.FromArgb(
       255,
       (int)(gradientStart.R * u + gradientEnd.R * t),
       (int)(gradientStart.G * u + gradientEnd.G * t),
       (int)(gradientStart.B * u + gradientEnd.B * t));
 
    return color;
}
 
Color[][] MapGradient(Color gradientStart, Color gradientEnd, float[][] perlinNoise)
{
   int width = perlinNoise.Length;
   int height = perlinNoise[0].Length;
 
   Color[][] image = GetEmptyArray(width, height);
 
   for (int i = 0; i < width; i++)
   {
      for (int j = 0; j < height; j++)
      {
         image[i][j] = GetColor(gradientStart, gradientEnd, perlinNoise[i][j]);
      }
   }
 
   return image;
}

Perlin noise can be used to blend between two textures, as shown in Figure 3. You should use Perlin noise with very high contrast to prevent textures from looking fuzzy. The following code snippet shows how to blend two images using Perlin noise.

Color[][] BlendImages(Color[][] image1, Color[][] image2, float[][] perlinNoise)
{
   int width = image1.Length;
   int height = image1[0].Length;
 
   Color[][] image = GetEmptyArray(width, height);
 
   for (int i = 0; i < width; i++)
   {
      for (int j = 0; j < height; j++)
      {
         image[i][j] = Interpolate(image1[i][j], image2[i][j], perlinNoise[i][j]);
      }
   }
 
    return image;
}

Image 1

Image 2

Perlin noise

Blend using noise

Figure 3

Of course, you would not create textures this way, but it can be used for interesting real time transitions. Figure 4 shows very cheap plant growth using only three textures and appropriate blending.

The following function computes a series of frames, a transition from one image to the other. We calculate a blend mask, and for each frame, we adjust the greys according to the frame number, so that the first frame gives a white blend mask, and subsequent blend masks become blacker, until the last one is completely black.

float[][] AdjustLevels(float[][] image, float low, float high)
{
   int width = image.Length;
   int height = image[0].Length;
 
   float[][] newImage = GetEmptyArray(width, height);
 
   for (int i = 0; i < width; i++)
   {
      for(int j = 0; j < height; j++)
      {
         float col = image[i][j];
 
         if (col <= low)
         {
             newImage[i][j] = 0;
         }
         else if (col >= high)
         {
            newImage[i][j] = 1;
         }
         else
         {
            newImage[i][j] = (col - low) / (high - low);
         }
      }
   }
 
   return newImage;
}
 
Color[][][] AnimateTransition(Color[][] image1, Color[][] image2, int frameCount)
{
   Color[][][] animation = new Color[frameCount][][];
 
   float low = 0;
   float increment = 1.0f / frameCount;
   float high = increment;
 
   float[][] perlinNoise = AdjustLevels(
      GeneratePerlinNoise(image1.Length, image1[0].Length, 9),
      0.2f, 0.8f); //initial adjustment gives more frames with action.
 
   for (int i = 0; i < frameCount; i++)
   {
      AdjustLevels(perlinNoise, low, high);
      float[][] blendMask = AdjustLevels(perlinNoise, low, high);
      animation[i] = BlendImages(image1, image2, blendMask);
      //SaveImage(animation[i], "blend_animation" + i + ".png");
      SaveImage(MapToGrey(blendMask), "blend_mask" + i + ".png");
      low = high;
      high += increment;
   }
 
   return animation;
}

Real time transitions using Perlin noise

Blend textures

Figure 4.

Landscape Generation

When Perlin noise is interpreted as a height map, an interesting terrain can be created (Figure 5).

Softimage Mod Tool is a free 3D modelling and animation application especially suited for games. One of its features is a built-in landscape generator that can use Perlin noise, among several others, to generate landscape meshes.

Height map generated from Perlin noise

Mesh generated from height map

Rendered mesh

Figure 5

Object Placement

Perlin noise can also be used to place objects on a grid more naturally than can be done with uniform random placement. To do this, follow these steps:

• Define k sets of similar looking objects.
• Create Perlin noise large enough to cover your grid. Each pixel of noise should correspond with one cell in the grid.
• For every cell in the grid, find the corresponding pixel of noise, and use the following formula to decide from which set you should choose an object: i = floor (n / (1.0 / k)). You choose objects from set S(i), usually randomly.

You can use this method even if you do not use a grid to place objects. Just define a grid so that there is roughly, on average, one object per cell. For every object to be placed, first determine the cell it corresponds to, and then proceed as above. If this requires a too large grid, you can use a smaller grid, so that there is more than one object per cell. Use linear interpolation to obtain a Perlin value for an object. You won’t get the Perlin pattern inside a grid cell – but it will hide the fact that there is a grid.

Figure 6 – In large worlds, the Perlin patterns can easily be seen. Here three sets of objects have been used: city, suburban, and industrial. (Art: Chris Cunnington)

For you to see the characteristic Perlin pattern, the world has to be quite large (Figure 6). However, you can benefit from Perlin placement even for small worlds. In a small world, there will be much more variation between successively generated worlds than there would be had they been generated by another method, as the images in Figure 7 illustrate.

Figure 7 – A big variety of small worlds. (Art: Chris Cunnington)

Sometimes you can construct your sets so that a certain property maps to the set number in an obvious way. For example, for sets of buildings, it would make sense to let the shortest buildings be in set 0, and the tallest buildings in the last set. Arranging your objects in this way ensures that very short buildings are never next to very tall buildings. This can enhance the illusion of “spatial progression”.

Sometimes there is no relationship between the set number and any property, and you benefit nothing from one set of objects always being close to objects in the same or adjacent sets. In this case, you can increase the amount of variety between different worlds by permuting the set indices, i.e., every time the algorithm runs, i = 0 will select objects from a different set. This can easily be accomplished by creating a shuffled array m containing the integers 0..k-1, and then choosing objects from the set S(m(i)).

It is very noticeable when two adjacent objects are the same, and this happens much more frequently with Perlin placement than with uniform random placement. There are three ways in which you can reduce or eliminate this effect:

1. Create more objects. To get the same number of adjacent objects in a grid as you would get with uniform random placement, you would need as many objects in a set as you would need in the entire collection for uniform random placement! If you have k sets, you will need to create k times the amount of art!
2. Another nifty trick is to further subdivide each set into “white” and “black” objects. The grid is then treated as a black and white checker board, and objects are placed so that “white” objects are always on “white” squares, and “black” objects always on “black” squares. This trick can be expanded to more than two colours, and non-periodic grid patterns, but is the subject of another article.
3. In some games, you can reduce the jarring effect by introducing small random transformations (rotation, scaling, mirroring, and for certain types of objects, shearing). This is especially effective for plants and other organic objects. You can also introduce small random colour variations, although you should take care not to destroy the overall colour and lighting of the game.

For this application, you might find that the first and last sets are under- represented. This has to do with the way Perlin noise generates more greys near the centre than it generates whites and blacks. The easiest way to rectify this problem, is to duplicate the under-represented sets.

The more sets you have, the smaller contiguous regions will be, and the more interesting your grid will be. If you have a small number of sets, you might wish to duplicate the sets for a more interesting world. Make sure that duplicate sets are not next to each other (for example, S[0] and S[1] must contain different elements) – otherwise this step will have no effect.

Be careful when tweaking a world generation parameter: remember that Perlin worlds look quite different from each other with the same parameter settings, something that can easily throw off any “trends”. Always run the algorithm a few times with the same settings to make sure what you perceive as a general occurrence is not an isolated anomaly.

Perlin Noise Tiles

Perlin noise can be made tileable by using a power of 2 for the array dimensions (128 × 128, for example).

You can also create a set of tiles by using a set of base noise arrays with the same first row and first column. All tiles in the set will tile smoothly with each other.

Perlin Noise Animation

The algorithm for generating Perlin noise is easily modified to make animation sequences. The basic idea is to generate a block of 3D Perlin noise, cut it in slices, and use each slice as an image of the animation sequence. If you use a power of two for the time dimension, the sequence will loop smoothly as well.

This sequence can be used for object placement to simulate transitions that will add life to your game.

The 3D version of the algorithm is quite slow – on my machine a lazy-man’s implementation takes about thirty minutes to produce 256 frames of a 256 × 256 image sequence.

Download

• C# Implementation
• Python Implementation

References

If you want to know more about Perlin noise, check out these handy sources for additional information on the subject.

• Atkins, M.; Barad H.; Gerlitz, O.; Goehring, D. Real-Time Procedural Texturing Techniques Using MMXMore texture generating techniques using Perlin noise.
• Elias, H. Perlin Noise.A very good introduction to Perlin noise.
• Gustavson, S. Simplex noise demystified.Explains classic Perlin noise, and an improvement thereof (simplex noise). The treatment is technical, but comes with very readable source code.
• Perlin, K. Makin Noise.The creator of Perlin noise’s website.
• Zucker, M. The Perlin noise math FAQ.A deeper look into the mathematics of Perlin noise.