Basic Collision Detection in 2D – Part 1

This article originally appeared in Dev.Mag Issue 28, released in January 2009.

Almost every video game needs to respond to objects touching each other in some sense, a practice commonly known as collision detection. Whether it’s simply to prevent the player character from walking through the walls of your maze with a simple collision grid array, or if it’s to test if any of the hundreds of projectiles fired by a boss character in a top-down shoot-’em-up have struck the player’s ship, your game will likely require a collision detection system of one sort or another.

So there comes a time in almost every game’s development cycle when an important choice needs to be made: how accurate should the collision detection be, and which method should be used to achieve that accuracy. This is a decision that is not made lightly, since it can drastically affect both gameplay and performance of your game.

Unfortunately, there’s often no avoiding the mathematics behind collision detection. However, anyone with so much as a secondary-school maths education will be able to follow the collision detection explanations in this article.

Bounding sphere/circle test

Sprite with circular collision bounds.

The simplest of all methods for detecting intersections between objects is a simple bounding sphere test. Essentially, this represents objects in the world as circles or spheres, and test whether they touch, intersect or completely contain each other. This method is ideal when accuracy is not paramount, for objects roughly circular in shape, or in instances where these objects do a lot of rotations.

Each object will have a bounding circle defined by a centre point and a radius. To test for collision with another bounding circle, all that needs to be done is compare the distance between the two centre points with the sum of the two radii:

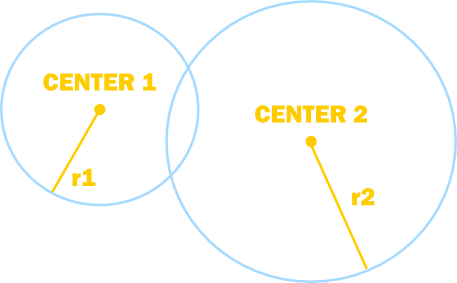
Circle-circle collision.

• If the distance exceeds the sum, the circles are too far apart to intersect.
• If the distance is equal to the sum, the circles are touching.
• If the distance is less than the sum of the radii, the circles intersect.

CircleCircleCollision
Input
	Center1	x/y pair of floating points	Centre of first circle
	R1	Floating point	Radius of first circle
	Center2	x/y pair of floating points	Centre of second circle
	R2	Floating point	Radius of second circle
Output
	True if circles collide
Method
	// Calculate difference between centres
	distX = Center1.X – Center2.X
	distY = Center1.Y – Center2.Y
	// Get distance with Pythagoras
	dist = sqrt((distX * distX) + (distY * distY))
	return dist <= (R1 + R2)

The above method can be optimized somewhat by comparing the square distance with the square of the sum of the radii instead, saving a comparatively slow square root operation, as shown below.

	// Get distance with Pythagoras
	squaredist = (distX * distX) + (distY * distY)
	return squaredist <= (R1 + R2) * (R1 + R2)

Bounding box test

Sprite with rectangular collision bounds.

The second obvious solution to the problem is to represent obstacles as axis-aligned rectangles. This method is ideal for smaller objects that are roughly rectangular and because it is incredibly fast to process.

The method that will be described uses a contradiction to determine whether the rectangles intersect. Because it is simpler instead to determine whether rectangles do notintersect, the function will calculate that and return the negation of its result.

Rectangles will be defined by their left-, top-, bottom- and right-edges. To determine whether two rectangles do not intersect, one simply has to check for any of the following conditions:

• Rectangle 1′s bottom edge is higher than Rectangle 2′s top edge.
• Rectangle 1′s top edge is lower than Rectangle 2′s bottom edge.
• Rectangle 1′s left edge is to the right of Rectangle 2′s right edge.
• Rectangle 1′s right edge is to the left of Rectangle 2′s left edge.

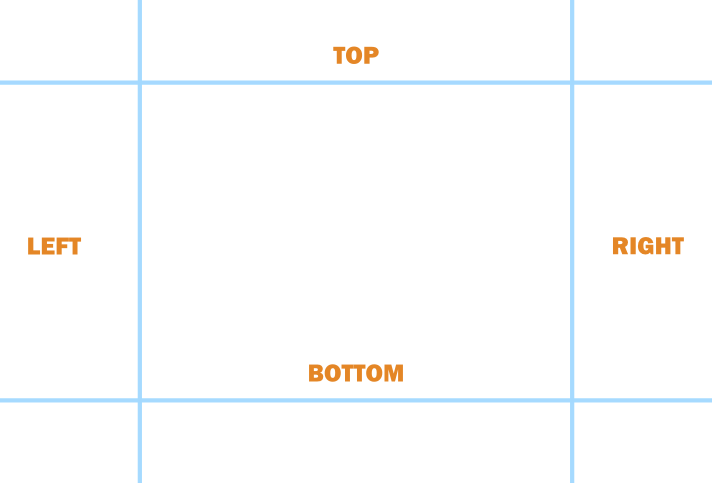
Bounding box collision.

RectRectCollision
Input
	Rect1	Rectangle	First Rectangle
	Rect2	Rectangle	Second Rectangle
Output
	True if the rectangles collide
Method
OutsideBottom = Rect1.Bottom < Rect2.Top
OutsideTop = Rect1.Top > Rect2.Bottom
OutsideLeft = Rect1.Left > Rect2.Right
OutsideRight = Rect1.Right < Rect2.Left
	return NOT (OutsideBottom OR OutsideTop OR OutsideLeft OR OutsideRight)

The above can then be condensed into a single line as follows.

	return NOT (
		(Rect1.Bottom < Rect2.Top) OR
		(Rect1.Top > Rect2.Bottom) OR
		(Rect1.Left > Rect2.Right) OR
		(Rect1.Right < Rect2.Left) )

Line-Line intersection test

Occasionally, one would need to represent objects in the game as simple lines (or perhaps a compound group of lines). Testing collision between two lines is slightly more complicated that the two methods described above, requiring some algebra to develop an algorithm, but is still otherwise fairly simple.

All lines used in this method will be represented as two points along the line (or the two endpoints if the lines are to be considered line segments instead of lines of infinite length). With a line \(A\) of infinite length, and two points on that line, \( A_1\) and \(A_2\), we define point \(P_a\), any point on line \(A\) as:

$$P_a = A_1 + u_a (A_2 - A_1),$$

with \(u_a\) being any real number.

That is, \(P_a\) is a point \(u_a\)-percent along the line from \(A_1\) to \( A_2\). Note that, since \(u_a\) is any real number, this point (and therefore the intersection between the lines) can lie on any point on either side of \(A_1\) and \(A_2\). Conversely, if \(u_a\)is between 0 and 1, \(P_a\) is between points \(A_1\) and \(A_2\) (this is important later).

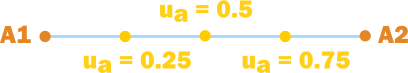
\(P_a\) for different values of \(u_a\)

Similarly, we define point \(P_b\), any point on line \(B\), as:

$$P_b = B_1 + u_B(B_2 - B_1),$$

with \(u_b\)being any real number and \(B_1\) and \(B_2\) as two points on line \(B\).

Solving for the point where \(P_a = P_b\) (the intersection between these lines), we get two equations:

$$x_{A_1} + u_a(x_{A_2} - x_{A_1}) = x_{B_1} + u_b(x_{B_2} - x_{B_1})$$

$$y_{A_1} + u_a(y_{A_2} - y_{A_1}) = y_{B_1} + u_b(y_{B_2} - y_{B_1})$$

Solving the above for \(u_a \) and \(u_b\) gives:

$$ u_a = \frac{(x_{B_2} - x_{B_1})(y_{A_1} - y_{B_1}) – (y_{B_2} - y_{B_1})(x_{A_1} – x_{B_1})}{(y_{B_2} - y_{B_1})(x_{A_2} - x_{A_1}) – (x_{B_2} - x_{B_1})(y_{A_2} - y_{A_1})}$$

$$ u_b = \frac{(x_{A_2} - x_{A_1})(y_{A_1} - y_{B_1}) – (y_{A_2} - y_{A_1})(x_{A_1} – x_{B_1})}{(y_{B_2} - y_{B_1})(x_{A_2} - x_{A_1}) – (x_{B_2} - x_{B_1})(y_{A_2} - y_{A_1})}$$

You’ll notice that the denominator for these two equations is the same. Thus, if the denominator is 0, both \(u_a\) and \(u_b\) are undefined, and no collision between these lines exist (the lines are parallel). The algorithm for simple infinite-line length checks simply needs to calculate the value for this denominator to determine whether a collision exists.

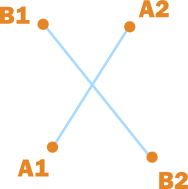
Line-line collision.

Input
	LineA1	Point	First point on line A
	LineA2	Point	Second point on line A
	LineB1	Point	First point on line B
	LineB2	Point	Second point on line B
Output
	True if lines collide
Method
	denom = ((LineB2.Y – LineB1.Y) * (LineA2.X – LineA1.X)) –
		((LineB2.X – lineB1.X) * (LineA2.Y - LineA1.Y))
	return denom != 0

However, there will be occasions when either one or both of the lines to be tested are not lines of infinite length. In this case, as mentioned above, \(u_a\)and \(u_b\) become really important. If \(u_a\) is between 0 and 1, then the collision occurs on a line segment of line \(A\), between points \(A_1\) and \(A_2\), and, similarly, if \(u_b\) is between 0 and 1, the collision occurs on a line segment of line \(B\), between points \(B_1\) and \(B_2\). More often than not, you’ll want to perform both these checks in your collision routine.

And that’s all we have space for this month. Next issue we’ll look at getting more information out of some of these collision routines, as well as covering a few more complicated algorithms.

Related posts

1. Basic Collision Detection in 2D – Part 2 This article originally appeared in Dev.Mag Issue 29, released in...
2. Basic Vector Recipes This tutorial covers basic algorithms with vectors....
3. Trigonometry: Part 1 This article originally appeared in Dev.Mag Issue 14, released in...
4. Trigonometry: Part 3 This article originally appeared in Dev.Mag Issue 16, released in...
5. On the Back of a Napkin: Part 3 This article originally appeared in Dev.Mag Issue 4, released in...
6. On the Back of a Napkin: Part 2 This article originally appeared in Dev.Mag Issue 3, released in...