In the article Bézier Curves for your Games: A Tutorial, I introduced Bézier curves and Bézier paths. In this tutorial I provide some algorithms useful for working with Bézier curves: determining the length of a piece of curve; interpolating a set of points with a Bézier path; and reducing a large point set to a smooth Bézier curve. (Image by snuffyTHEbear).
Calculating curve length
Assuming that the line segments we use for drawing are a reasonable representation of our curve, we can estimate the curve length by summing the lengths of the segments. These can be added together to get the length of a Bézier path.
A more complicated strategy is necessary when we need the length of only a part of the curve, and not the complete curve.
First, we must cache the accumulative length of segments when we update the drawing points. For example, if the lengths of the first three segments of a curve are 2, 3 and 1, the accumulative lengths are 2, 5, and 6.
Then, we can use a simple subtraction to find the length of the piece of the curve (assuming, for a moment, that we need it only between points that coincide with the drawing points). For example, to find the length of curve between drawing points 5 and 8, we do the following calculation:
accumulativeLength[8] – accumulativeLength[5 – 1] //wrong |
Note that we subtract 1 from the smaller index. To prevent us from having to handle a special case, we can start the accumulative lengths with 0. The accumulativeLengths array is then one larger than the drawingPoints array. With this scheme, we calculate the length between drawing points 5 and 8 as follows:
accumulativeLength[8 + 1] – accumulativeLength[5] //correct |
If we need to calculate the length between arbitrary points (not just drawing points), then we need a slightly more complicated scheme, as in the following function:
//Calculates the length of curve between two points on the curve CalculateLenth(segmentIndex0, t0, segmentIndex1, t1) { //assert(segmentIndex0 <= segmentIndex1) if(segmentIndex0 == segmentIndex1) { assert(t1 >= t0); } p0 = getPoint(curveIndex0, t0); beginningLength = (drawingPoints[segmentIndex0 + 1] – p0).Length; p1 = getPoint(curveIndex1, t1); endLength = (drawingPoints[segmentIndex1] – p1).Length; length = beginningLength + endLength; if(segmentIndex0 != segmentIndex1) { midLength = accumulativeLength[segmentIndex0 + 2] – accumulativeLength[segmentIndex1]; length += midLength; } return length; } |
The code in red above samples the curve directly to calculate the two points. However, this will give results inconsistent with our approximation using line segments of the midLength. It is often not a problem, since the difference might be small. If it is a problem, you can use points on the line segments instead of points on the curve to calculate the approximation.
This technique is consistent with the approximation of the interior segment, and is somewhat faster. All you have to do is use the following method to calculate p0 and p1, instead of using the getPoint method as above.
GetPointOnSegment(curveIndex, t) { return (t – 1) * points[curveIndex] + t * points[curveIndex + 1]); } |
Constructing a smooth Bézier path from a set of points
Two related problems arise frequently when working with paths. Both problems require us to find an aesthetic, smooth curve for a set of points.
The first problem occurs when only a few points of the curve are given, and we have to find a smooth curve that passes through all the points. One example of this is the paths given to AI agents. A walking character looks very funny when abruptly turning to follow the path laid out by the AI designer or algorithm. Using a bit of smoothing greatly enhances the believability of the character’s movements. This is interpolation.

An example of Bézier interpolation.
The second problem occurs when a vast number of points are given, and we need to simplify the curve without distorting the overall shape. This, for example, is useful to make a curve in a line drawing game more pleasing to the eye, and easier for the AI to follow. This is simplification.

An example of Bézier simplification.
Bézier interpolation
The challenge is to find a nice, smooth curve passing through all the points given in order. We can think of this as smoothing a curve made out of line segments. A Bézier path is smooth if each endpoint and its two surrounding control points lie in a straight line. In other words, the two tangents at each Bézier endpoint are parallel.
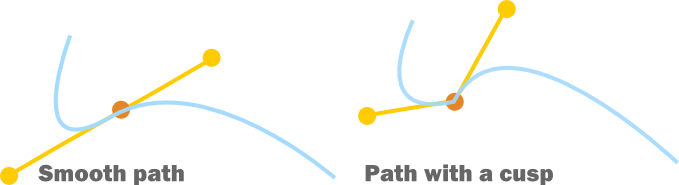
These figures show two Bézier paths, each made out of two Bézier curves. The yellow line segments are tangents to the left and right of the orange Bézier endpoint. When the tangents are parallel, as on the left, the connection between the two Bézier curves is smooth. If they are not parallel, as on the right, there is a cusp where the curves connect.
For now, let us assume the segments are roughly of the same length.
The basic idea is to calculate control points around each endpoint so that they lie in a straight line with the endpoint. We make this line parallel to the line formed with the neighbouring Bézier endpoints, and we make the control points the same distance from the endpoint that they surround (for now). We use a scaling parameter to control curvature of the curve at the Bézier endpoint. Curves for different scale values are shown below.
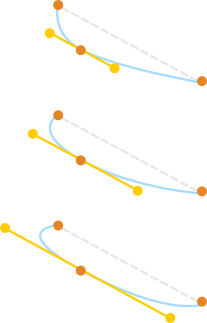
We are given the orange points. The algorithm calculates the yellow points, which in this case are the control points around the Bézier endpoint in the middle. We do it so that the yellow points that surround a Bézier endpoint lie in a straight line. We can tweak the distance of the control points from this Bézier endpoint with a parameter. The larger this parameter, the smaller the curvature at that Bézier endpoint. In these images, each of the three Bézier paths has two Bézier curves.
The basic steps to calculate the two control points around a point p1, are the following, where p0 and p2 are the endpoints around p1:
tangent = (p2 – p0).normalized; q0 = p1 - scale * tangent; q1 = p1 + scale * tangent; |
The tricky bit is handling the first and last control points of the path. These are calculated as before, except that we use the two first or two last endpoints to do the tangent calculation.
We can now iterate through all the segment points, and calculate control points depending on the correct case.
List<Vector3> Interpolate(List<Vector3> segmentPoints, float scale) { controlPoints = new List<Vector3>(); if (segmentPoints.Count < 2) { return; } for (int i = 0; i < segmentPoints.Count; i++) { if (i == 0) // is first { Vector3 p1 = segmentPoints[i]; Vector3 p2 = segmentPoints[i + 1]; Vector3 tangent = (p2 - p1); Vector3 q1 = p1 + scale * tangent; controlPoints.Add(p1); controlPoints.Add(q1); } else if (i == segmentPoints.Count - 1) //last { Vector3 p0 = segmentPoints[i - 1]; Vector3 p1 = segmentPoints[i]; Vector3 tangent = (p1 - p0); Vector3 q0 = p1 - scale * tangent; controlPoints.Add(q0); controlPoints.Add(p1); } else { Vector3 p0 = segmentPoints[i - 1]; Vector3 p1 = segmentPoints[i]; Vector3 p2 = segmentPoints[i + 1]; Vector3 tangent = (p2 - p0).normalized; Vector3 q0 = p1 - scale * tangent * (p1 - p0).magnitude; Vector3 q1 = p1 + scale * tangent * (p2 - p1).magnitude; controlPoints.Add(q0); controlPoints.Add(p1); controlPoints.Add(q1); } } return controlPoints; } |
Bézier simplification (Quick and Dirty Method)
If we would also like to reduce the number of points in our curve, it is much harder to construct a suitable Bézier curve, especially if we want the best possible fit given constraints on the number of control points and degree of the curve. There is a quick and dirty method that works well in many cases. Here is the broad outline:
- Add points to a list so that successive points are as far apart as possible, within a specified minimum.
- Use Bézier interpolation discussed above.
The algorithm to perform step 1 works as follows:
- We add the first point from our list of source points to the list sample points.
- We set the next potential sample point as the second point in the list of source points.
- We then iterate through the remaining source points (starting at the third point). For each point, we check whether the last sample point added is outside a minimum square distance of that point. If it is, we add the potential sample point to the list of sample points. The current point becomes the new potential sample point (regardless of whether the last test failed).
Here is the code:
samplePoints.Push(sourcePoints[0]); Vector3 potentialSamplePoint = sourcePoints[1]; int i = 2; for (i = 2; i < sourcePoints.Count; i++ ) { if(((potentialSamplePoint - sourcePoints[i]).sqrMagnitude > minSqrDistance) && ((samplePoints.Peek() - sourcePoints[i]).sqrMagnitude > maxSqrDistance)) { samplePoints.Push(potentialSamplePoint); } potentialSamplePoint = sourcePoints[i]; } |
The last bit of the curve is a bit messy to handle. We can either throw the last point away, and lose a small piece of the curve; or add the last point as a control point, and keep the full curve.
If we decide to add the last point, the last two points in samplePoints may lie very close to each other. If this is the case, you might either discard the second last point, or move it a bit further from the last point, closer to the third last point. The exact best new location for this point is a bit tricky to calculate. The following is an approximation scheme:
Let p0, p1 be the last two sample points, and p2 be the last potentialSamplePoint (which is also the last point from samplePoints). We want to calculate a new position for p1.
tangent = (p0 – p2).normalized; d2 = (p2 – p1).magnitude; d1 = (p1 – p0).magnitude; p1 = p1 + tangent * ((d1 - d2)/2); |
I based the approximation above on the following reasoning:
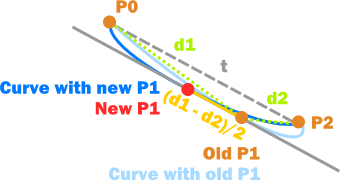 The vector t is an approximate tangent vector for the curve at p1. This is the same tangent as would be calculated by our smoothing algorithm. We then want to move p1 so that it lies on this tangent, (passing through the original p1), and lies roughly the same distance from p0 and p1. Instead of calculating exact intersections, we approximate the desired distance as half the sum of the original distances, that is, the new distance from p1 to p0 (and p2) is given by (d1 + d2) / 2. Now p1 is already d2 from p2, so we subtract that from (d1 + d2) / 2 to obtain (d1 – d2) / 2. This is exact only when all three points lie in a straight line, but it is close enough in other cases.
The vector t is an approximate tangent vector for the curve at p1. This is the same tangent as would be calculated by our smoothing algorithm. We then want to move p1 so that it lies on this tangent, (passing through the original p1), and lies roughly the same distance from p0 and p1. Instead of calculating exact intersections, we approximate the desired distance as half the sum of the original distances, that is, the new distance from p1 to p0 (and p2) is given by (d1 + d2) / 2. Now p1 is already d2 from p2, so we subtract that from (d1 + d2) / 2 to obtain (d1 – d2) / 2. This is exact only when all three points lie in a straight line, but it is close enough in other cases.
The final algorithm is this:
public List<Vector3> SamplePoints(List<Vector3> sourcePoints, float minSqrDistance, float maxSqrDistance, float scale) { if(sourcePoints.Count < 2) { return; } Stack<Vector3> samplePoints = new Stack<Vector3>(); samplePoints.Push(sourcePoints[0]); Vector3 potentialSamplePoint = sourcePoints[1]; int i = 2; for (i = 2; i < sourcePoints.Count; i++ ) { if(((potentialSamplePoint - sourcePoints[i]).sqrMagnitude > minSqrDistance) && ((samplePoints.Peek() - sourcePoints[i]).sqrMagnitude > maxSqrDistance)) { samplePoints.Push(potentialSamplePoint); } potentialSamplePoint = sourcePoints[i]; } //now handle last bit of curve Vector3 p1 = samplePoints.Pop(); //last sample point Vector3 p0 = samplePoints.Peek(); //second last sample point Vector3 tangent = (p0 - potentialSamplePoint).normalized; float d2 = (potentialSamplePoint - p1).magnitude; float d1 = (p1 - p0).magnitude; p1 = p1 + tangent * ((d1 - d2)/2); samplePoints.Push(p1); samplePoints.Push(potentialSamplePoint); return Interpolate(samplePoints.ToArray(), scale); } |
Once we have reduced the points, the final step is to make the curve smooth, by using Bézier interpolation. We simply pass the list returned by SamplePoints to the Interpolate function.
The algorithm is easily converted to an online algorithm. If the curve is drawn while the sampling is being done, the potential point should be included for drawing to make the curve building smooth. If it is not, the curve end will jump as the curve is extended. The end of the curve will also adjust itself as the curve is extended; unfortunately, there is not much that can be done about this.
If the last samples being too close present a problem, we can perform the end-of-curve calculations where the curve is drawn. We also need to do the calculations once the last sourcePoint has been given.
void SamplePointsOnline(Vector3 newSourcePoint, float minSqrDistance) { //samplePoints and potentialSamplePoint are now fields if(samplePoints.Empty) { samplePoints.Push(newSourcePoint); } else if(samplePoints.Count == 1) { potentialSamplePoint = newSourcePoint; } else { if((samplePoints.Back() – newSourcePoint).sqrMagnitude >= minSqrDistance) { segmentPoint.Push(potentialSamplePoint); } potentialSamplePoint = sourcePoints[i];; } } |
Downloads
(WARNING: The code fairy stole all the comments in these files!)
- Bezier Curves (64 KB, Unity 3D Project, zipped)
- BezierPath.cs (C# source code file)
Hi Herman
Thanks for this awesome tut. I just wanted to know if the download is the smooth included? When I open the download, I get a warning that my Unity is too old, can that cause the interpolate to work incorrectly, surely not?
Thanks again
Hi Tiaan,
The file does include smoothing (
InterpolateorSamplePoints), but I see you have to make the constantSEGMENTS_PER_CURVEquite high to get good results (start by trying1000). I have not tested it with older versions of Unity, but the general algorithms should still work; I am not sure if the LineRenderer has changed much, but you should be able to get everything to work.Hi Herman,
great tutorial! unfortunately, I don’t know C#, I work mainly in C and C++. Do you have the sample code available in C++?
Unfortunately, I don’t. If you use STL with C++, and have some kind of 3D vector class, it should translate fairly well. Just replace C# List with STL vector, and use the equivalent methods. Similarly replace Vector with whatever 3D vector you are suing, and substitute equivalent operations.
You are my hero. Very good explanation. Inspiring to let my self share my knowledge to other. Thanks
Hi Herman
Awesome tutrorial! I translated code in Java and run on android device,but FPS low to 9-10 fps :(. Are you can get advice, how change algorithm to increase the speed of smoothing?
Thanks
Hey just tried out your project and am having some issues. The “scale” parameter seems fairly unusable. It seems to make jagged and wonky line segments as it approaches 1.0. The code itself doesn’t seem very versatile, filled with magic numbers and the like. I figured the input for the building of the bezier curve would be based on the number of points desired. I assume scale tries to perform that action, but it seems bugged. Please correct me if I’m wrong, I don’t fully understand your implementation yet so forgive me if I’m mistaken. Any help would be appreciated. Also, as someone else mentioned, this will not perform very well given its multitude of Lists and the fact that it rebuilds every query.
Pingback: Bézier Path Algorithms – wiki.kukool.cn
Is there a mathematical way to cut a bezier curve at a certain t-value and find the 2 resulting curves?
The only solution I can think of is to first calculate 6 equally spaced points along each section of the curve and then generate new curves using an interpolation of those points. The first problem I have with this method is that it will get close but never exactly match the original curve. The other problem is that it also uses a lot more computing power than some sort of a formula would.
So, is there a smarter way to do this?
I too am interested in any solution to this problem.
Since you know where you cut, you know the P0 and P3 points of any of the two new segments. Only the P1 and P2 are left to determine, which can be solved as a system of 2 equations to 2 unknowns (for each new segment). As example, if you cut at 0.6 the initial curve, then, for the first segment, you need to solve:
8/27 P0 + 4/3 P1 + 2/3 P2 + 1/27 P3 = P( initial at t = 0.2)
1/27 P0 + 2/3 P1 + 4/3 P2 + 8/27 P3 + P( initial at t=0.4 )
where P0 is the starting point for the initial (and the first) segment, and P3 is the point where you cut the curve. The two unknown values are P1 and P2, for the new first segment. The magic number 0.2 is one third of the initial t-span values making now the first segment, 1/3 * 0.6; while 0.4 = 2/3 of that span, that is, 2/3 * 0.6.
For the second segment, same equations on the left side, but now, P3 = ending point of both the initial and the new second segment, while P0 = the cutting point. The right side members are now P(initial at t= 0.6 + 1/3*0.4) and P( initial at t= 0.6 + 2/3 * 0.4), where 0.4 is the initial “span” of the initial t values which will make the second segment ( from 0.6 to 1.0, that is, a t span of 0.4).
Yes, you can find the equations here
Pingback: Unity Learning Resources – Next Numen
Some bezier math papers I release recently: http://microbians.com/?page=math
In cocos-2dx I can schedule a path with given control points in a given time using ccBezierConfig, but i want to schedule a group of paths as we did in iOS using UIBezeirPath by adding group of paths.please help asap
Hi Herman Tulleken,
I want draw simple line with watercolor effect, but I’m not succeed.
your suggestion is great helpful to me.
Thanks,
D @ 🙂
Pingback: Aprenda a fazer Curvas de Bézier para os seus games |